【贪心算法】局部最优解 纯理论
贪心算法
贪心算法,顾名思义,选当前最好的结果,不去考虑未来的结果。从局部最优解到全局解。
贪心算法,最终的解有可能不是最好的解,贪心只是保证了有这么一个解存在,如果要找到全局最优解,可以用其他的策略,比如动态规划,backtracking等。
贪心算法的应用场景有很多。在小学的时候,数学老师就问过我们,做包子要十分钟,洗衣机洗衣服要二十分钟,洗碗又要十分钟,问你要先做哪个。这里就有一个贪心的运用,人做事能并行,在洗衣机洗衣服的时候,可以先把包子做了,再把碗洗了。这样子的时间刚好来到了二十分钟,衣服也洗碗了。
三件完成的事为20分钟。
在这里,局部最优解为先洗衣机,再包子再希望。从一步步的角度来看,一开始的选择正确,后面的也选择正确,直接就达到了一个正确的解,但是这个解有可能不是最优解。可能存在另外一种解法。
又比如一个很经典的背包问题。
背包问题
说是有这么一个背包,背包有一个最大承重为W,背包里有n个物品,每个物品的重量为wi,价值为vi。问你如何选择物品放入背包,使得背包的总价值最大。这里讨论的背包问题里的物品可被分解,不可被分解的背包问题在数学界中还没有被证明
举个例子
背包最大承重为12
有三个物品,分别重量为6,5,2 价值为49,40,20
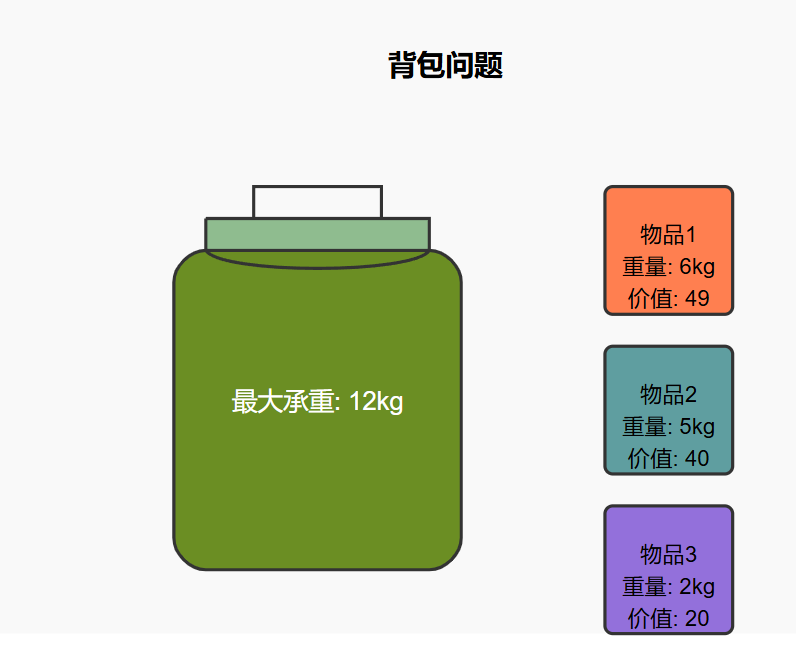
现在要求你去选择物品放入背包,使得背包的总价值最大。
你会怎么去选择呢?
解法1 最大价值
选择价值最大的物品放入背包,剩下的空间再放入其他的物品。
在这里,答案是 先放入6,再放入5,最后放入2。由于6+5=11,最后一个物品的重量为2,无法放入,需要对物品3进行分解,放入1/2的物品3,最后的总价值为49+40+10=99
解法2 最大重量
因为物品1的重量为重,价值也为最高,我们可以选择放入5/6的物品1,剩下的空间放入物品2和物品3,这时候的总价值为5/6*49+40+20=100.8
背包也刚好的达到了最大的容量,是不是很神奇,居然比第一个解答还有更好的答案,但是我说,还有更好的解法你会怎么想?
解法3 特定物品(value/weight) 最大价值比
先放入物品1,再放入4/5的物品2,最后放入物品3,背包的总价值来到了49+4/5*40+20=101. 真是神奇,居然比第二个解法还要好上一筹。
从这三个解法中我们可以看出来,每一种解法都是贪心算法的一种变量,在只看到了第一种解法的情况下,我们可能会认为这个解法是最优解,但是在后面的解法中,我们发现了更好的解法。我们又一次的证明了贪心算法的局部最优解并不一定是全局最优解。
好,那么不难发现,贪心算法,无非就是一个特定的选择过程,只要选择对,最后的解就一定是对的,只不过不能保证是最优解。回到代码层面,不过是不同的sort方法而已。
再讲一个例子
例子2
有这么一个matriz,其中1代表此路可通,0不通,初始坐标为0,0,终点为(x-1, y-1),也就是5,4
可以向右→,下↓和斜着走,每一步的权重都为1,无论怎么走,都是一样的权重
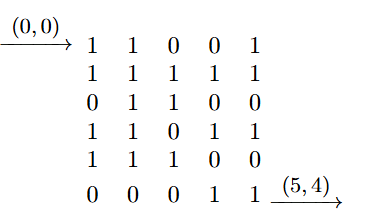
好,现在问题来了,你应该怎么走才是最优解呢?换一种说法,怎么走才能到达终点的路径最短呢?
聪明的你肯定想到了,只要我一直斜着走,如果路都为1,斜着走的路径就一定是最短的,但是如果路上有0呢?这时候随机一下就好了,因为权重都是一样的,向右和向下的权重都是1,斜着走的权重也是1,所以无论怎么走,都是一样的。
我们可以用贪心算法来解决这个问题。
一直斜着走,如果斜着走不通,就向下走,如果向下也不通,就向右走,如果都不通,代表此题无解。很简单对吧
那么怎么保证这个结果就一定是最优解呢?好像还真的保证不了喔,贪心只是保证有这么一个解法存在,没有去证明就是最优解。
这是贪心的第一种策略,一直斜着走。
还有其他几种策略,还有距离优先,动态权重,目标导向折扣等等一类的策略。
这里就不展开了。
这里有一道很经典的leetcode题目,有兴趣的可以尝试一下,很简单,只要理解了贪心的思想这类题都是一样的,不过是不同的sort方法而已。
结束
让我们说谢谢贪心。
谢谢贪心